

quaternion의 angle은 radian으로 정보를 받고 있음
- 3.14의 값이 써진다면 각도는 180도
실제 각도를 써서 보는 게 더 직관적이므로
radians function을 활용
180 degree = 3.1415... radian = 𝝅 = $PI
float angle = radians(chf("angle"));
vector axis = chv("axis");
@orient = quaternion(angle, axis);이렇게 하고 angle 값에 180을 입력하면 180도 회전하게 만들 수 있음

axis에 angle을 곱해주는 게 아니라 rand 값과 noise의 값을 각각 곱해줘서 결과를 확인해보면
rand는 0에서 1 사이의 무작위한 값을 도출, 프레임마다 다른 각도, 각각의 점들이 모두 무작위의 결과를 가짐
noise는 0에서 1 사이 값이 패턴을 가짐, 시간에 지남에 따라 꿀렁꿀렁 회전하는 느낌
0도, 90도, 180도, 270도의 값을 각각 얻어내기 위해서
1) noise에 4를 곱해서 0에서 4 사이의 값이 나오도록 만들어줌
2) floor() 나 trunc() 을 써줘서

값들이 정수로 나오도록 만들어주기
0,1,2,3으로 값이 도출됨
프레임마다 똑딱똑딱 움직이게 됨
3) *$PI/2 (90도를 곱해줌) 를 해서 값이 0, 90, 180, 270이 되도록

4를 곱하기 전에
@A = fit(@A,0.4,0.6,0,1); 를 해주면 적극적으로 노이즈가 움직이는 것처럼 보임
0.5를 기준으로 그 주변이 가장 많이 움직이게 되기 때문
@A = chramp("TWA",@A); 로 그래프를 움직여서 원하는 느낌을 찾아줄 수도 있음


@P.y의 값도 변경해서 키보드 타이핑하는 느낌도 만들어줄 수 있음
4. 실제 각도값을 오리엔트의 값으로 변환하는 법


여기서 rot 옆에 쓰인 0의 의미는
x,y,z 순서로 각도를 회전시키겠다는 뜻
이 순서가 중요해지는 날이 오게 됨... 미래에...
5. 오리엔트값을 믹스(블랜드)해주는 법
lerp
1) float을 쓸 때
lerp(0,10,0.1) = 1
0에서 10까지에서 0.1만큼의 비율 1
2) vector를 쓸 때
vector A = {0,0,0}, vector B = {2,4,6}
Vector C = lerp(A,B,0.5) = {1,2,3}
lerp의 마지막 input은 0에서 1사이의 amount 값을 써주면 됨
slerp(vector4, vector4, float)
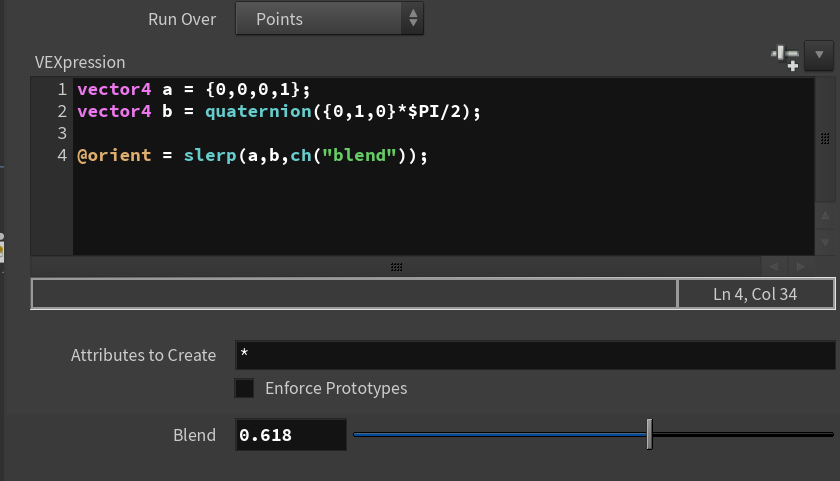
blend의 값이 0이면 a, 1이면 b의 값이 나타남

blend에 @Time%1을 넣어 반복되서 돌아가게,
채널램프 값으로 적용시킬 수도 있음


blend의 값이 0이면 base의 값이 나오고, 1이면 target의 값이 나옴
target은 위에서 만들었던 프레임마다 똑딱거리며 돌아가는 모션\
이 둘을 blend 해서 스무스하게 돌아가게 만들어줌
그래프를 바꾸면서 느낌 보기
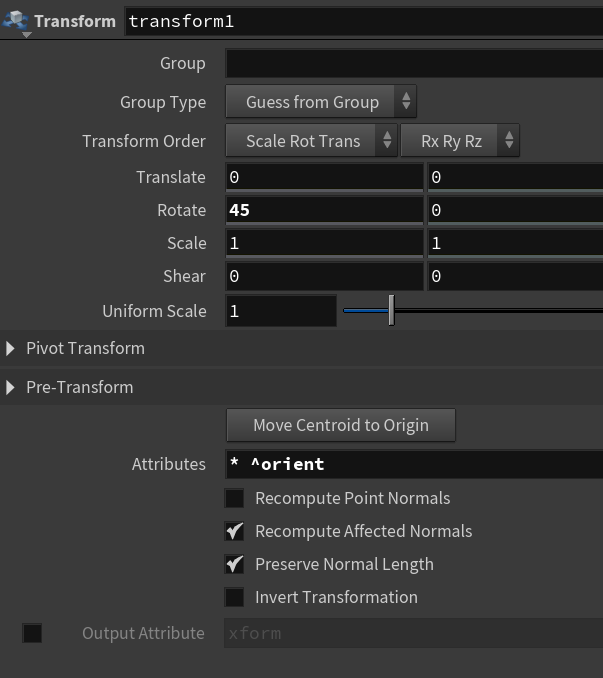

attribute wrangle 아래에 transform을 달아서 회전시키면 전체가 통으로 회전되는데,
attribute에 ^orient를 써주면 우측의 결과가 된다.
attribute wrangle 위에 transform을 달아서 회전시키면 그냥 오른쪽의 결과가 된다.
6. 오리엔트 값끼리의 곱, 효과의 중첩
qmultiply
slerp(A,B,0.2) 면 Ax0.2 + Bx0.8 이라면
qmultiply(A,B)는 A+B


angle 값이 0이면 위에서 정의한 @orient의 결과가 나타나고, (돼지들이 노말방향을 향해 바라보고 있는 모습)
angle 값이 높아질수록 돼지들은 아래를 바라보는 느낌이 됨


headshake 변수를 추가
0,1,0 축을 기준으로 시간에 따라 20도씩 회전한다는 의미가 됨. 3을 곱해줘서 더 빨리 도리도리하도록
sin(@Time) 값은 -1에서 1 사이의 값을 반환하여 20도가 -20에서 20 이 되도록
wobble 변수를 추가
돼지들마다 다르게 noise 먹여줌, z축을 기준으로 회전되어 갸우뚱 됨
7. 오리엔트 값을 매트릭스로, 매트릭스 값을 오리엔트로
qconvert

@orient를 다시 matrix로
@orient와 matrix는 상호관계에 있음
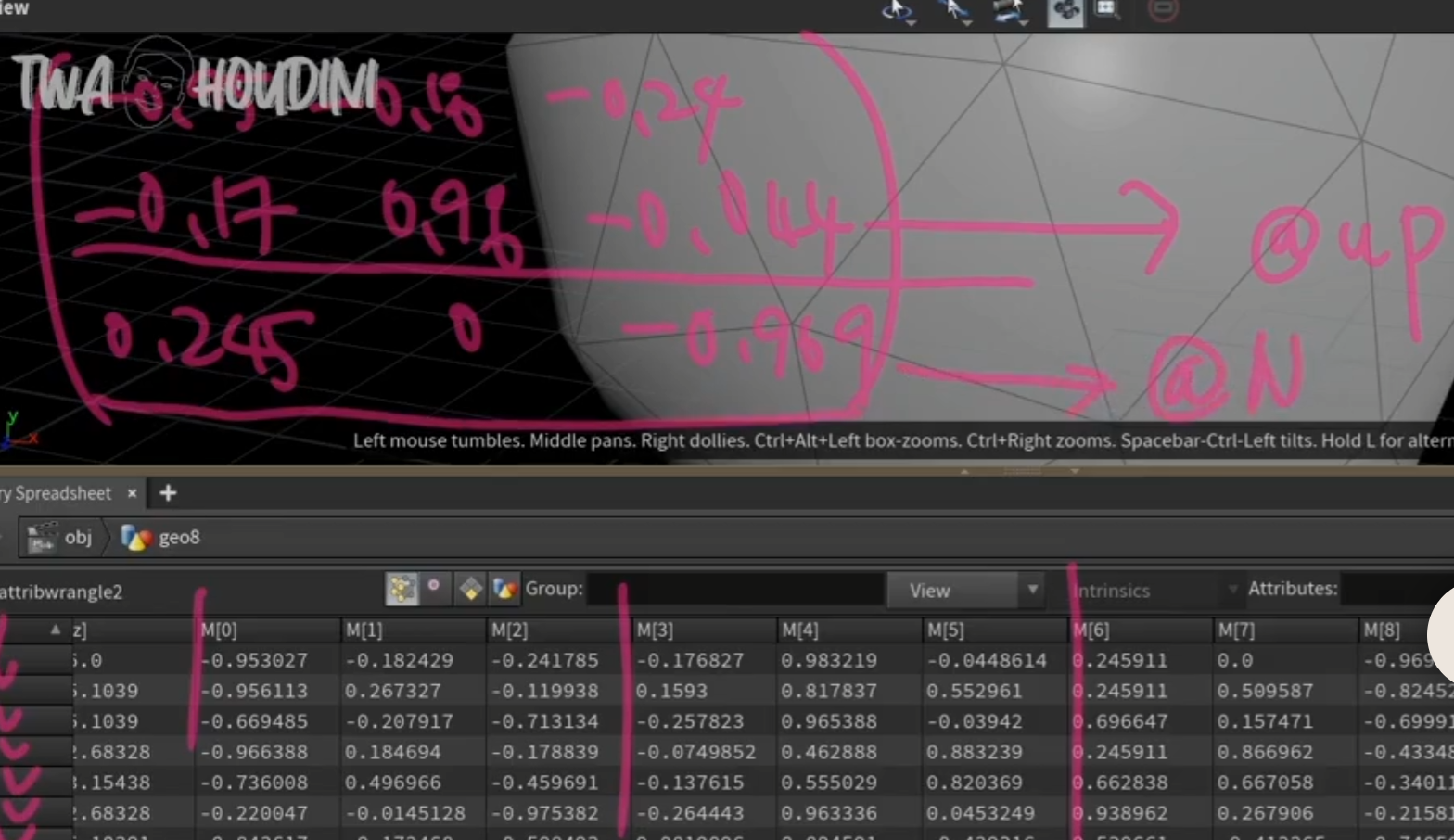
8. 오리엔트에서 얻어낸 매트릭스값에서 @n과 @up만 따로 뽑아내는 법

의 결과는 (g,h,i)이다. @N
{0,1,0} 을 곱했을 때는 (d,e,f) @up
A[ ] = [{a,b,c}, {d,e,f},{g,h,i}]
A[0] = {a,b,c}
matrix3 m = qconvert(@orient);
@N = {0,0,1}*m;
@up = {0,1,0}*m; matrix3 m = qconvert(p@orient);
vector axes[] = set(m);
@N = normalize(axes[2]); // z axis
@up = normalize(axes[1]); // y axis
하나 하나씩 설명을 들었을 때는 이해가 되는데 뭔가 전체적으로 파악하기가 어려운 느낌이다.😥
@N 과 @up 설명강의부터 다시 들어봐야겠다..!
'Joy of Vex' 카테고리의 다른 글
| Joy of Vex [Day18] (2) | 2023.03.04 |
|---|---|
| Joy of Vex [Day17-1,2] (0) | 2023.03.01 |
| Joy of Vex [Day16] (0) | 2023.02.28 |
| Joy of Vex [Day15] (0) | 2023.02.27 |
| Joy of Vex [Day14] (0) | 2023.02.23 |



